Посмотрите это видео на Rutube: «FFT - Fast Fourier Transform»
Давайте разберем поверхностно еще один важный термин, смысл которого нужно знать каждому меломану хотя бы в общих чертах. Это аббревиатура FFT или БПФ, что означает «быстрое преобразование Фурье».
Мы разбирали с вами всевозможные графики представления аудиосигнала: синусоиду, которая упрощенно представляет сигнал в виде кривой, которая показывает амплитуду сигнала в определенный момент времени.
Мы недавно разобрали АЧХ, где временной шкалы нет, но зато есть частотная шкала и амплитуда. Глядя на АЧХ, мы понимаем какие частоты, с какой амплитудой присутствуют в сигнале или звуковой волне в комнате прослушивания. То есть, синусоида показывает время, а АЧХ частоту (помимо амплитуды).
Музыка представляет собой сложный сигнал, длящийся во времени с различным набором частот (каждая со своей амплитудой), который состоит из огромного количества синусоид и косинусоид, которые влияют друг на друга в определенные моменты времени и формируют более сложный график, чем простая синусоида.
Кроме того, синусоида не дает информации о той или иной частоте сложного сигнала в определенный момент времени. А амплитудно-частотная характеристика, имеет горизонтальную ось частот, а вот со временем не дружит вообще.
Поэтому аудио инженеры задумались над решением задачи, которое позволило бы наблюдать музыкальный сигнал сразу в трех областях: амплитуды, частоты и времени. То есть, мы можем увидеть какая частота, на какой миллисекунде имеет ту или иную амплитуду.
На помощь приходит математика и ее яркий представитель – месье Жозеф Фурье, который в 1822 году выдал в свет свою знаменитую концепцию «рядов Фурье». На основе этой математической модели инженерам в 1967 году удалость создать алгоритм быстрого преобразования Фурье для разложения музыкального сигнала на составляющие элементы (амплитуды, частоты и фазы) в реальном масштабе времени.
Основная идея преобразования Фурье заключается в том, что любой сложный сигнал (не только аудио) можно представить в виде суммы простых синусоидальных волн разной частоты, амплитуды и фазы. Алгоритм использует комплексные числа для представления этих синусоидальных волн и вычисляет амплитуду и фазу каждой составляющей.
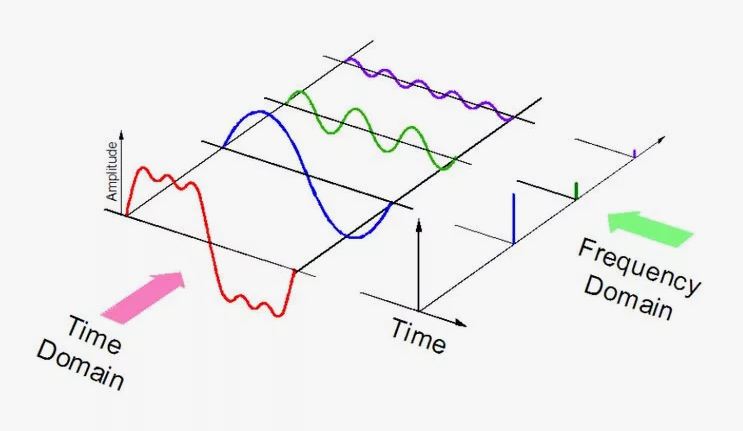
Проще говоря, БПФ переводит сигнал из временной области в частотную. На видео вверху это показано в простой форме. Благодаря всему этому, мы можем наблюдать, анализировать и редактировать аудио сигнал в трех измерениях (спектральный анализ).
Сын лавочника Жозеф Фурье, который служил в армии Наполеона и принимал участие в египетском походе 1798 года, даже и не предполагал, что его математическая модель позволит потомкам редактировать музыку, создавать системы шумоподавления, формировать алгоритмы распознавания визуальных объектов и много другое.
10 июня 1815 года Наполеон назначил Фурье пенсию в размере 6 тысяч франков, но Фурье не получил её ни разу, так как к 1 июля Наполеон был свергнут. После этого Фурье вернулся в Париж, где некоторое время работал директором Статистического бюро, а в 1817 году стал членом Академии.
Имя ученого увековечено в общепринятом названии выражения, отображающего зависимость в установившемся режиме между плотностью потока энергии, передающейся посредством теплопроводности, и градиентом температуры: эта формула известна как закон теплопроводности Фурье.

